The Most Comprehensive Guide to Risk-Free Option Arbitrage Operations: Even Warren Buffett is Using

The pricing mechanism of options is complex, and there are many opportunities for risk-free arbitrage. Well-known ones include option parity conversion arbitrage, bull-bear spread arbitrage, and convexity arbitrage strategies. As more and more people participate in options trading, the arbitrage space of simple arbitrage strategies is continuously squeezed, while relatively complex arbitrage strategies still have relatively large arbitrage space due to higher participation thresholds.

Using option contracts on the underlying asset instead of spot trading in an arbitrage portfolio has great advantages. It can not only reduce transaction costs but also complete the construction of the arbitrage portfolio in the option market, making the operation more convenient.

In addition, spot purchases require full funds. The maximum leverage of securities lending is no more than 2.5 times. The leverage of futures, which is about five times, can improve the efficiency of fund usage.

Arbitrage is the act of capturing profits from the unreasonable pricing of underlying assets by constructing asset portfolios.

In actual operation, the biggest characteristic of arbitrage is that the theoretical profit level is locked in when the portfolio is constructed. No matter how the price of the underlying asset changes, the arbitrage portfolio can obtain a cash flow greater than 0, that is, truly risk-free.

In addition, in a stricter sense, the return of an arbitrage portfolio does not change with the change in the price of the underlying asset. In other words, arbitrage is an absolute return product, and arbitrage portfolios are usually also hedge strategy portfolios.

Is risk-free option arbitrage possible?

Theoretically, in an efficient market, all market information will be reflected in prices immediately. No asset price will deviate from its proper value. Therefore, there should be no opportunity for risk-free arbitrage using price differences.

However, a large amount of research and practical experience shows that the real market is not a completely efficient market. There may be imbalances between different asset prices in an extremely short time, making risk-free arbitrage possible.

From the empirical evidence of international markets, currently, the arbitrage opportunities and spaces in mature markets are relatively limited. However, due to the insufficient maturity of emerging markets, there are still a large number of arbitrage opportunities.

However, as more and more investors participate in arbitrage and institutional automated trading systems mature, the arbitrage opportunities and spaces in emerging markets will also continue to decrease.

From the experience of international mature markets, seizing arbitrage opportunities in the later stage mainly depends on lower transaction costs and higher order placement speeds. Currently, only market makers or professional traders in mature markets have the resources to obtain option arbitrage opportunities.

The main types of US stock options are American options. Hong Kong stock options mainly use European options. The main difference between American options and European options lies in the flexibility of exercise time.

American options are options that can be exercised at any time before and on the expiration date. This means that the holder of the option has the right to decide to exercise the option at any time during the entire validity period of the option contract. This flexibility provides greater freedom for the holder, especially in cases where the price of the underlying asset fluctuates greatly.

European options can only be exercised on the expiration date. Whether the option is a call option or a put option, the holder must wait until the option expires to decide whether to exercise. This means that the option holder cannot lock in profits in advance, even if the price of the underlying asset changes significantly before the option expires.

The pricing of European options usually uses the Black-Scholes model, which is one of the most commonly used option pricing models in the financial field. Since European options can only be exercised at expiration, their mathematical pricing is relatively simpler, so this model is applicable to European options.

For American options, due to the possibility of early exercise, the pricing model will be more complex and need to consider the possibility of early exercise in various different scenarios.

Implementation of the Black-Scholes Option Pricing Formula

In Python programming, The Black-Scholes option pricing formula is implemented through the black_scholes_call and black_scholes_put functions. The perpetual option formula is implemented through integrating option prices and using the everlasting_call and everlasting_put functions.

Theoretically, in an efficient market, all market information will be reflected in prices immediately. No asset price will deviate from its proper value. Therefore, there should be no opportunity for risk-free arbitrage using price differences.

However, a large amount of research and practical experience shows that the real market is not a completely efficient market. There may be imbalances between different asset prices in an extremely short time, making risk-free arbitrage possible.

From the empirical evidence of international markets, currently, the arbitrage opportunities and spaces in mature markets are relatively limited. However, due to the insufficient maturity of emerging markets, there are still a large number of arbitrage opportunities.

However, as more and more investors participate in arbitrage and institutional automated trading systems mature, the arbitrage opportunities and spaces in emerging markets will also continue to decrease.

From the experience of international mature markets, seizing arbitrage opportunities in the later stage mainly depends on lower transaction costs and higher order placement speeds. Currently, only market makers or professional traders in mature markets have the resources to obtain option arbitrage opportunities.

Principles of Risk-Free Option Arbitrage

In the following, taking European options as an example, we assume that the underlying asset does not pay dividends during the option holding period. In the calculation process, relevant transaction costs and opportunity costs of margin are not considered. At the same time, it is assumed that interest rates will not change during the option’s lifespan and that borrowing and lending rates are equal.

Let’s first review the four most basic option strategies:

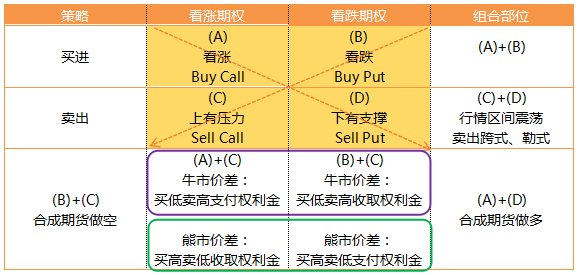
1.Vertical spread strategy: Refers to an investor buying one option while simultaneously selling another option. These two options have the same underlying asset and the same expiration date but different strike prices.

Types of vertical spreads

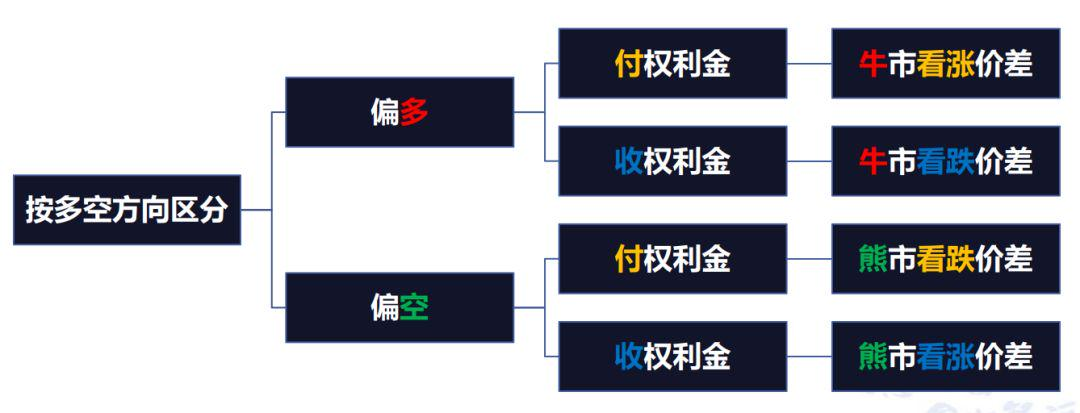
The same is true for doing spreads. Whether you are bullish or bearish, there are both paying and receiving option premiums. When forming a bull spread using call options, you must pay option premiums. When forming a bear spread using put options, you can receive option premiums. When doing a single leg and being bullish, there are two directions: one is to buy a call option, and the other is to sell a put option. Buying a call option is paying option premiums, and selling a put option is receiving option premiums. Similarly, when doing a single leg and being bearish, there will also be paying and receiving option premiums. But at this time, buying a put option is paying option premiums, and selling a call option is receiving option premiums.

2.Single option upper limit arbitrage

At any time, the price of a call option cannot exceed the price of the underlying asset. That is, the upper limit of the option price is the price of the underlying asset. If the price of a call option exceeds the price of the underlying asset, you can sell the call option and simultaneously buy the underlying asset at the current price to obtain risk-free profits.

For European put options, at any time, their price should be lower than the present value of their strike price. If the price of a put option is higher than the present value of its strike price, you can sell the put option and simultaneously buy the underlying asset equal to the present value of its strike price.

The profit and loss curve of single option upper limit arbitrage is similar to moving the profit and loss curve of selling a put option entirely above the 0-axis. In actual operation, futures of the underlying asset can also be used to replace spot of the underlying asset to achieve more convenient operation and lower transaction costs.

3.Single option lower limit arbitrage

At any time, the price of a European call option without dividends should be higher than the larger of the difference between the current price of the underlying asset and the present value of the strike price and zero.

If the difference between the current price of the underlying asset and the present value of the strike price is greater than 0 and the price of the call option is lower than the difference between the current price of the underlying asset and the present value of the strike price, then call option lower limit arbitrage can be performed. That is, buying a call option and simultaneously selling the underlying asset to obtain risk-free profits.

The profit and loss curve of call option lower limit arbitrage is similar to moving the profit and loss curve of buying a put option entirely above the 0-axis. Similarly, the price of a European put option without dividends should be higher than the larger of the difference between the present value of the strike price and the current price of the underlying asset and zero. If the difference between the present value of the strike price and the current price of the underlying asset is greater than 0 and the price of the put option is lower than the difference between the present value of the strike price and the current price of the underlying asset, then put option lower limit arbitrage can be performed. That is, buying a put option and simultaneously buying the underlying asset to obtain risk-free profits. In short, it is “buy low and sell high.”

The profit and loss curve of put option lower limit arbitrage is similar to moving the profit and loss curve of buying a call option entirely above the 0-axis.

From another perspective, the meaning of option lower limit arbitrage is that the option price should be greater than the larger of its intrinsic value and zero. The value of an option is composed of intrinsic value and time value. Among them, the intrinsic value of an option is the profit that the buyer can obtain immediately by exercising.

4.Put-call parity arbitrage

The option parity relationship means that there is an equilibrium relationship between call options and put options with the same strike price at any time. That is, for call and put options with the same underlying asset, same expiration date, and same strike price, at a specific time, the difference between the call option and the put option should be equal to the difference between the current price of the underlying asset and the present value of the option strike price.

The establishment of this equation is based on the assumptions of the B-S model and can be proved by the combined cash flows under different prices of the underlying asset.

We can regard the difference between the call option and the put option as portfolio A and the difference between the current price of the underlying asset and the present value of the option strike price as portfolio B. When A≠B, we can obtain the price difference between the two by buying low and selling high.

The profit and loss curve of put-call parity arbitrage is a horizontal straight line and is located above the 0-axis.

5.Put-call and futures parity arbitrage

The put-call and futures parity theory is evolved from the put-call parity theory. It replaces the spot in the original put-call parity theory with futures. This theory was proposed by Tucker in 1991 mainly to solve the high cost and inconvenient operation of put-call parity arbitrage.

This theory believes that there will also be a specific equilibrium relationship between futures prices and option prices. That is, the sum of the call option price and the present value of the option strike price (regarded as portfolio A) should be equal to the sum of the put option price and the present value of the underlying asset futures price (regarded as portfolio B). When A≠B, we can obtain the price difference between the two by buying low and selling high.

The profit and loss curve of put-call and futures parity arbitrage is similar to that of put-call parity arbitrage. It is also a horizontal straight line and is located above the 0-axis.

(1) Vertical spread upper limit arbitrage The upper limit relationship of call option spreads means that the present value of the difference between the higher strike price and the lower strike price (regarded as portfolio A) should be greater than or equal to the difference between the call option price of the lower strike price and the call option price of the higher strike price (regarded as portfolio B).

The upper limit relationship of put option spreads means that the present value of the difference between the higher strike price and the lower strike price (regarded as portfolio A) should be greater than or equal to the difference between the put option price of the higher strike price and the call option price of the lower strike price (regarded as portfolio B).

(2) Vertical spread lower limit arbitrage The profit and loss curve of call option vertical spread lower limit arbitrage is similar to moving the profit and loss curve of a bull spread combination entirely above the 0-axis.

The profit and loss curve of put option vertical spread lower limit arbitrage is similar to moving the profit and loss curve of a bear spread combination entirely above the 0-axis.

Option convexity spread arbitrage uses the convex relationship of options to conduct arbitrage.

The profit and loss curve of convexity spread arbitrage is similar to moving the profit and loss curve of a butterfly spread combination entirely above the 0-axis.

(3) Box spread arbitrage Box spread arbitrage, also known as box arbitrage, is composed of a bull spread combination and a bear spread combination. The box spread relationship is established on the no-arbitrage principle between bull spread options and bear spread options.

The profit and loss curve of box (box) spread arbitrage is a horizontal straight line and is located above the 0-axis.

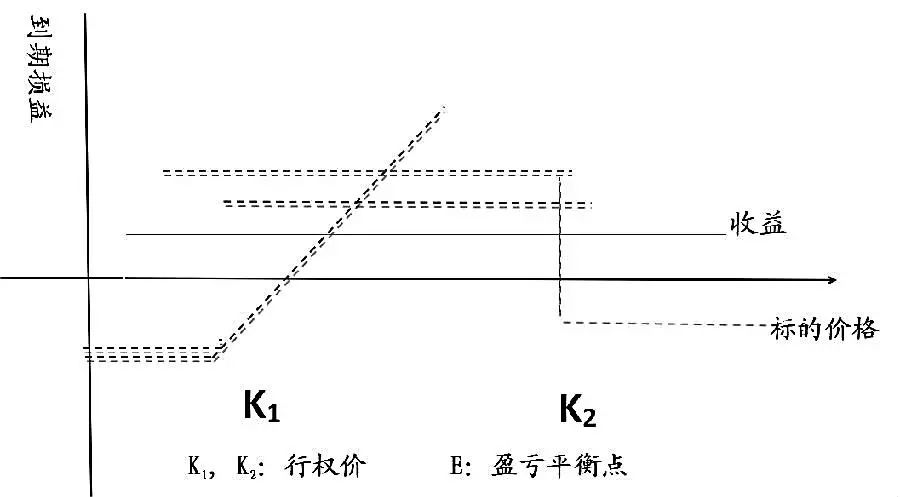
Simply put, when the strike price is K1, buy a call option and simultaneously sell a put option. When the strike price is K2, buy a put option and simultaneously sell a call option. In this way, synthetic long futures with a cost of F1 and synthetic short futures with a cost of F2 are replicated respectively. In theory, the costs of replicating long and short futures from option contracts of the same maturity are equal, that is, F1 = F2. In reality, however, the market price of option contracts often deviates from the theoretical price. Therefore, the profit of box spread arbitrage is the difference between |F1 - F2|.

Summary

In addition, there are several key points to note:

1.Calculation of arbitrage space The actual arbitrage profit should be the balance after deducting the above expenses from the theoretical arbitrage profit. Transaction costs mainly include option transaction costs and execution costs when execution is required, as well as transaction costs for futures and spot. Among them, since the impact cost accounts for a relatively small proportion and is actually difficult to estimate, we will not discuss it in detail.

ETF transactions belong to stock transactions, and their transaction costs are usually relatively high. If shorting spot is required in an arbitrage strategy, it needs to be realized through securities lending, and the transaction cost will be even higher. Therefore, the impact of ETF transaction costs on actual arbitrage profits needs to be considered carefully.

Such high costs will undoubtedly have a greater impact on arbitrage profits and even lead to many arbitrage opportunities not being triggered.

2.Which is better, options or spot? If spot of the option’s underlying asset is selected for arbitrage, operations usually need to be carried out in both the stock market and the futures market, which will undoubtedly increase the operational difficulty and transaction risk.

In addition, spot purchases require full funds. The maximum leverage of securities lending is no more than 2.5 times. The leverage of options, which is about five times, can improve the efficiency of fund usage.

By making good use of the above rules, we can practice what we have learned on compliant US stock and derivative trading platforms such as Interactive Brokers, Charles Schwab, BiyaPay, etc., try investing in options of related underlying assets to obtain objective returns and hedge risks.